235. Lowest Common Ancestor of a Binary Search Tree

Easy
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Given binary search tree:  root = [6,2,8,0,4,7,9,null,null,3,5]

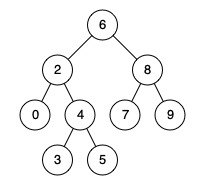
Example 1:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Note:
  • All of the nodes' values will be unique.
  • p and q are different and both values will exist in the BST.
Idea:
preorder (top down) to find p,q. LCA is the node when split happen.
1. if the root value is both larger than node p and q, LCA is in left subtree.
2. if the root value is both smaller than node p and 1, LCA is in right subtree.
otherwise, there is a split or the first present node of node p,q.


    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null)
            return null;
        if(root.val > p.val && root.val > q.val){
            return lowestCommonAncestor(root.left, p, q);
        }
        if(root.val < p.val && root.val < q.val){
            return lowestCommonAncestor(root.right, p, q);
        }
        return root;//where split happened
    }

Comments

Post a Comment

Popular posts from this blog

MockInterview:785. Is Graph Bipartite?

Medium Given an undirected  graph , return  true  if and only if it is bipartite. Recall that a graph is  bipartite  if we can split it's set of nodes into two independent subsets A and B such that  every edge in the graph has one node in A and another node in B. The graph is given in the following form:  graph[i]  is a list of indexes  j  for which the edge between nodes  i  and  j  exists .  Each node is an integer between  0  and  graph.length - 1 .  There are no self edges or parallel edges:  graph[i]  does not contain  i , and it doesn't contain any element twice. Example 1: Input: [[1,3], [0,2], [1,3], [0,2]] Output: true Explanation: The graph looks like this: 0----1 | | | | 3----2 We can divide the vertices into two groups: {0, 2} and {1, 3}. Example 2: Input: [[1,2,3], [0,2], [0,1,3], [0,2]] Output: false Explanation: The graph looks...
Read more

geeksforgeeks:findFind zeroes to be flipped so that number of consecutive 1’s is maximized

Given a binary array and an integer m, find the position of zeroes flipping which creates maximum number of consecutive 1’s in array. Examples : Input: arr[] = {1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1} m = 2 Output: 5 7 We are allowed to flip maximum 2 zeroes. If we flip arr[5] and arr[7], we get 8 consecutive 1's which is maximum possible under given constraints Input: arr[] = {1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1} m = 1 Output: 7 We are allowed to flip maximum 1 zero. If we flip arr[7], we get 5 consecutive 1's which is maximum possible under given constraints. Input: arr[] = {0, 0, 0, 1} m = 4 Output: 0 1 2 Since m is more than number of zeroes, we can flip all zeroes. Input: arr[] = {0 , 0, 0, 0, 0} m = 2 Solution:  sliding window use a window covering from the wL to wR. Let variable zeroCount to count the zero numbers inside the window. If zero count of the current window is less than m, wide the window to right. update the widest wi...
Read more

94.Binary Tree Inorder Traversal

Image
94 .  Binary Tree Inorder Traversal Given a binary tree, return the  inorder  traversal of its nodes' values. Example: Input: [1,null,2,3] 1 \ 2 / 3 Output: [1,3,2] Ideas: 1 use stack to store the back pointer. 2 when the node n is not null, add this node into stack, look for its left node first. so push the left node.    when the node is null, pop the node from stack, visit this node first, then look for its right node.     if the node is null and stack is empty, break the iteration.     public List<Integer> inorderTraversal(TreeNode root) {         Stack<TreeNode> stack = new Stack<TreeNode>();         TreeNode head = root;         List<Integer> res = new ArrayList<Integer>();         while(true){             if(head!=null){         ...
Read more